13 oldala van egy újonnan felfedezett alakzatnak, ami ismétlődések nélkül tud lefedni egy nagyobb felületet
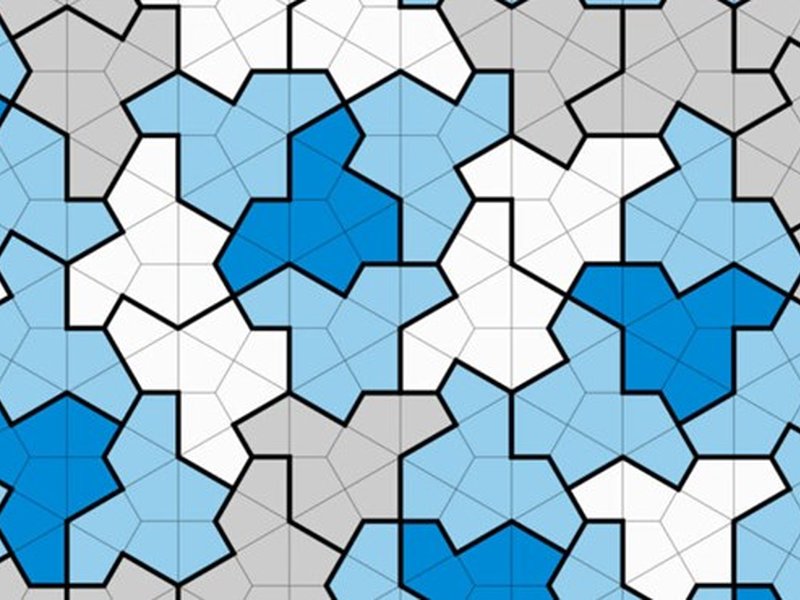
Egy olyan, 13 oldalas alakzatot fedeztek fel matematikusok, melynek mintázata sosem ismétlődik – a kutatók ezt „kalapnak” (hat) nevezték el.
Az új forma az „einstein” első ismert példája, amivel úgy lehet lefedni csempével egy felületet rések vagy átfedések nélkül, hogy az sosem fog ismétlődni – a tudósok fél évszázada kerestek egy ilyen, úgynevezett aperiodikus alakzatot, és abban sem voltak biztosak, hogy ilyen létezik. Az „einstein” elnevezés nem a híres fizikusra utal, hanem a német „ein stein”-re, ami magyarul azt jelenti, hogy „egy kő”.
Az alakzatot David Smith, egy nem hivatásos matematikus azonosította, aki a kapcsolódó tanulmányát – amiben szakképzett matematikusokkal működött együtt – az arXiv folyóiratban publikálta.
David Smith és csapata két módon is bizonyították, hogy ez az aperiodikus alakzat egy einstein. Ezek egyike, hogy észrevették: a „kalapok” nagyobb csoportokba rendeződnek, melyek aztán még tovább tudnak rendeződni, egy hierarchikus struktúrában. Kiderült: az új alakzattal történő csempézés képes egy végtelen síkot a mintázat ismétlődése nélkül kitölteni.
A második bizonyítás azon a tényen alapult, hogy ez a kalap egy nagyobb alakzat egy nagyobb folytonosság része. Az oldalak hosszának változtatásával tudták bizonyítani, hogy a kalap nevű alakzatot nem lehet periodikus – azaz ismétlődő – mintázatba rendezni.
Az új felfedezés az anyagtudományban is indíthat el új kutatásokat, hasonló felfedezésekért korábban Nobel-díjat is átadtak már.
A Science News idézte Craig Kaplant, a tanulmány társszerzőjét, aki szerint a kutatóknak folytatniuk kell a további einsteinek keresését – szerinte a mostani felfedezés után új alakzatokat is felfedezhetnek majd.